|
Once elevations are given by  . where x and y are Cartesian co-ordinates, local topographic variables are functions of first- (p and q),
second- (r, t, and s), and third-order (g, h,
k, and m) partial derivatives of elevation: . where x and y are Cartesian co-ordinates, local topographic variables are functions of first- (p and q),
second- (r, t, and s), and third-order (g, h,
k, and m) partial derivatives of elevation:
 , ,  ; ;
 , ,  , , 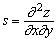 ; ;
 , ,  , ,  , ,  . .
To
compute partial derivatives of elevation from DEMs based on plane square
grids, one can use methods including an approximation of partial
derivatives by finite differences with the 3 x 3 plane square-gridded
moving windows (e.g., the Evans method).
In our
method, the third-order polynomial

is fitted by the least-squares approach to the 25
points of the 5 x 5 square-spaced window with a grid spacing of w:

The Cartesian coordinates and
elevations of the topographic surface are known for 25 points of this
window: (‑2w, 2w, z1), (‑w, 2w, z2),
(0, 2w, z3), (w, 2w, z4),
(2w, 2w, z5), (‑2w, w, z6),
(‑w, w, z7), (0, w, z8),
(w, w, z9), (2w, w, z10),
(‑2w, 0, z11), (‑w, 0, z12),
(0, 0, z13), (w, 0, z14),
(2w, 0, z15), (‑2w, ‑w, z16),
(‑w, ‑w, z17), (0, ‑w, z18),
(w, ‑w, z19), (2w, ‑w, z20),
(‑2w, ‑2w, z21), (‑w, ‑2w, z22),
(0, ‑2w, z23), (w, ‑2w, z24),
and (2w, ‑2w, z25). For the point (0, 0, z13), the polynomial coefficients (which are
partial derivatives of elevation) are estimated by the following formulae:

 , ,

 , ,

 , ,

 , ,

 , ,

 , ,

 , ,

 , ,

 . .
Moving the 5x5 window along a DEM, one can
calculate values of g, h, k, m, r, t, s,
p, and q (and so values of local morphometric variables) for
all points of the plane square-gridded DEM, except for two boundary rows
and two boundary columns on each side of the DEM.
References
Florinsky,
I.V., 2009. Computation of the third-order partial derivatives from a
digital elevation model. International
Journal of Geographical Information Science, 23: 213–231. doi pdf
For
details and examples, see:
|

|
DIGITAL TERRAIN ANALYSIS
IN SOIL SCIENCE AND GEOLOGY
2nd revised edition
I.V. Florinsky
Elsevier / Academic Press, 2016
Amsterdam, 486 p.
ISBN 978-0-12-804632-6
Contents Summary
ScienceDirect
|
|