|
Once elevations are given by  . where x and y are Cartesian co-ordinates, local topographic variables are functions of first- (p and q)
and second-order (r, t, and s) partial derivatives of
elevation . where x and y are Cartesian co-ordinates, local topographic variables are functions of first- (p and q)
and second-order (r, t, and s) partial derivatives of
elevation
 , ,  , ,  , ,  , , 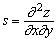 . .
Digital
models of local morphometric variables are usually derived by methods based
on the approximation of partial derivatives of elevation by finite
differences. Such methods have been developed and intended to calculate
partial derivatives from DEMs based on plane square grids (e.g., the Evans
method and IF-2009 method). However, a plane
square grid and a spheroidal equal angular grid have principally different
geometry. Therefore, it is obvious that methods developed for plane square
grids cannot be applied on spheroidal equal angular grids.
In our
method, the second-order polynomial

is fitted by the least-squares approach to the nine
points of the 3 x 3 spheroidal equal angular window:

The orthogonal spheroidal
coordinates and elevations are known for the window points (‑c, e, z1),
(0, e, z2),
(c, e, z3),
(‑b, 0, z4),
(0, 0, z5),
(b, 0, z6),
(‑a, ‑d, z7),
(0, ‑d, z8),
and (a, ‑d, z9). For the point (0, 0, z5), the polynomial coefficients (which are
partial derivatives of elevation) are estimated by the following formulae:
 , ,





 , ,
 , ,
 , ,





 . .
Moving the 3 x 3 window along a DEM, one can
calculate values of r, t, s, p, and q
(and so values of local morphometric variables) for all points of the
spheroidal equal angular DEM, except for boundary rows and columns on each
side of the DEM. If one processes a virtually closed, global spheroidal
equal angular DEM, it is possible to estimate values of topographic
variables in each point of such a DEM.
Values
of a, b, c, d, and e vary depending on
the latitude. Since geographic coordinates are known for every point of a
spheroidal equal angular grid, so a, b, c, d,
and e are easily calculated, for example, by well-known formulae
from the solution of the inverse geodetic problem for short distances.
Reference
Florinsky, I.V., 1998.
Derivation of topographic variables from a digital elevation model given by
a spheroidal trapezoidal grid. International
Journal of Geographical Information Science, 12: 829–852. doi pdf
Florinsky, I.V., 2017. Spheroidal equal angular DEMs:
The specificity of morphometric treatment. Transactions in GIS, 21:
1115–1129. doi pdf
For
details and examples, see:
|

|
DIGITAL TERRAIN ANALYSIS
IN SOIL SCIENCE AND GEOLOGY
2nd revised edition
I.V. Florinsky
Elsevier / Academic Press, 2016
Amsterdam, 486 p.
ISBN 978-0-12-804632-6
Contents Summary
ScienceDirect
|
|