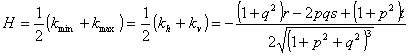|
en ru |
Mean curvature (H) is a half-sum of curvatures of
two orthogonal normal sections of the topographic surface at the given point*.
The unit of measurement is m-1. Once
elevations are given by
where
kmin, kmax, kh,
and kv are minimal, maximal, horizontal,
and vertical curvatures, correspondingly; Mean
curvature presents convergence and relative deceleration of gravity-driven flows
(controlled by horizontal and vertical curvatures, correspondingly) with
equal weights. Like other local morphometric
variables, mean curvature can be derived from a digital elevation model (DEM) by finite-difference
methods (e.g., IF-2009
method and IF-1998
method) as well as the universal spectral
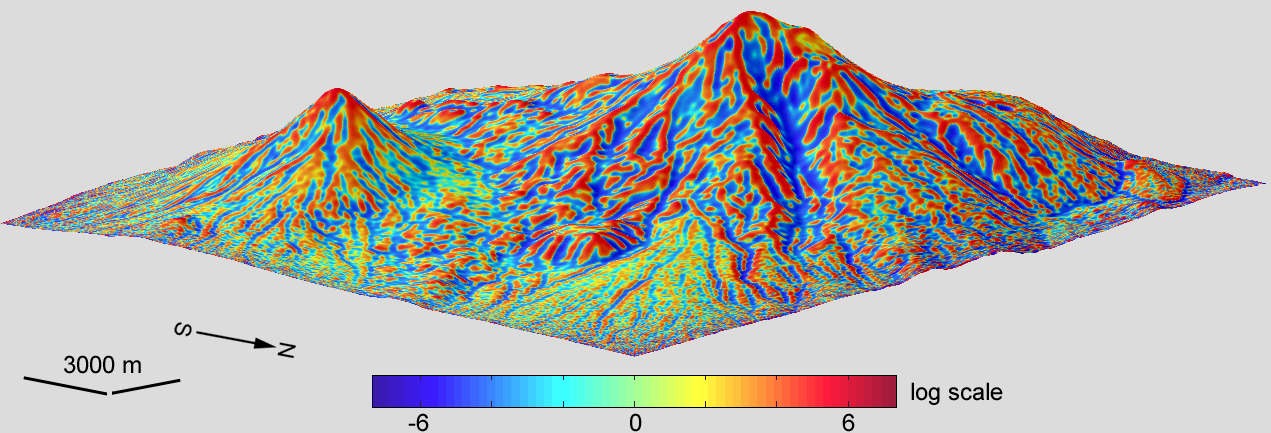
analytical method. Example**. A model of mean curvature was derived from a
DEM of Mount Ararat by the
universal spectral analytical method.
The model includes 779,401 points
(the matrix 1081 x 721); the grid spacing is 1". To deal
with the large dynamic range of this variable, its values were logarithmically transformed. The vertical
exaggeration of the 3D model is 2x. The data processing and modelling were carried out using the software Matlab R2008b. |
|
DIGITAL TERRAIN ANALYSIS IN SOIL SCIENCE AND GEOLOGY 2nd revised edition I.V. Florinsky Elsevier / Academic Press, 2016 Amsterdam, 486 p. ISBN 978-0-12-804632-6 |